Diagrama de Transición y Tabla de Transición (Autómatas)

UN DIAGRAMA DE TRANSICIONES es una colección finita de círculos, los cuales se pueden rotular para fines de referencia, conectados por flechas que reciben el nombre de ARCOS. 

Cada uno de estos arcos se etiqueta con un símbolo o categoría de símbolos que podría presentarse en la cadena de entrada que se analiza. Uno de los círculos se designa con un apuntador, y representa una posición inicial. Además, por lo menos uno de los círculos se representa como un círculo doble; estos círculos dobles designan posiciones del diagrama en las cuales se ha reconocido una cadena valida.

DIAGRAMA DE TRANSICIONES DETERMINISTA

• En particular, cada estado de estos diagramas solo debe tener un arco que sale para cada símbolo del alfabeto; de lo contrario, una maquina que llega a este estado se enfrentara a una elección de cuál debe ser el arco a seguir.
• Además, dicho diagrama debe estar completamente definido, es decir debe existir por lo menos un arco para cada símbolo del alfabeto; de lo contrario, una maquina que llega a este estado puede enfrentarse a una situación donde no pueda aplicarse ninguna transición.

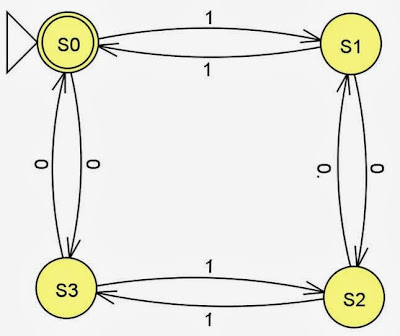
DT, Diagrama de Transiciones de ejemplo

Decimos que una cadena de símbolos es aceptada por un diagrama de transiciones si los símbolos que aparecen en la cadena (de izquierda a derecha) corresponden a una secuencia de arcos rotulados que conducen del círculo designado por el apuntador a un círculo doble. 

Los círculos de un diagrama de transiciones representan posiciones, o estados, donde no podemos encontrar al evaluar una cadena de símbolos. Es común llamar estados a los círculos de un diagrama de transiciones. Él circulo de partida se llama estado inicial y los círculos dobles, estados de aceptación.

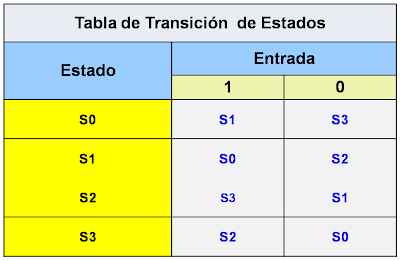
TABLA DE TRANSICIONES

Una tabla de transiciones es un arreglo (o matriz) bidimensional cuyos elementos proporcionan el resumen de un diagrama de transiciones correspondiente.   

TT, Tabla de Transiciones Correspondiente al DT anterior

Las cadenas que deben analizarse en una aplicación están construidas a partir de un conjunto de símbolos. En cualquier situación encontramos que el conjunto de símbolos es finito, por lo que nuestro primer paso hacia la formalización del proceso de reconocimiento es asumir la hipótesis de la existencia de una conjunto finito, no vacío, de símbolos a partir del cual se construyen las cadenas que se analizaran.   A este conjunto de símbolos lo llamamos alfabeto.

Cada cadena que se recibe se analizara como una secuencia de símbolos, uno a la vez. 

Nos referimos a la fuente de esta secuencia como el flujo de entrada conforme llega cada símbolo del flujo de entrada, nuestro proceso de reconocimiento implica cambiar de un estado, tomando de entre una cantidad finita de ellos, a otro, o bien permanecer en el estado actual.  El nuevo proceso dependerá únicamente del estado actual y del símbolo del que se recibe.

Para representar un programa en el mecanismo de control utilizamos un diagrama de transiciones cuyos estados representan los estados de la maquina y cuyos arcos representan una posible transición de la maquina. Por lo tanto, los estados de inicio y aceptación del diagrama corresponden a los estados de inicio y aceptación del autómata.

Un diagrama para un AFD aceptara l si y solo si su estado inicial es también un estado de aceptación.

El requisito del determinismo impone ciertas restricciones sobre los diagramas de transiciones que pueden aparecer en los programas para un autómata finito determinista.   Se dice que un diagrama de transiciones es determinista si cumple las siguientes condiciones:

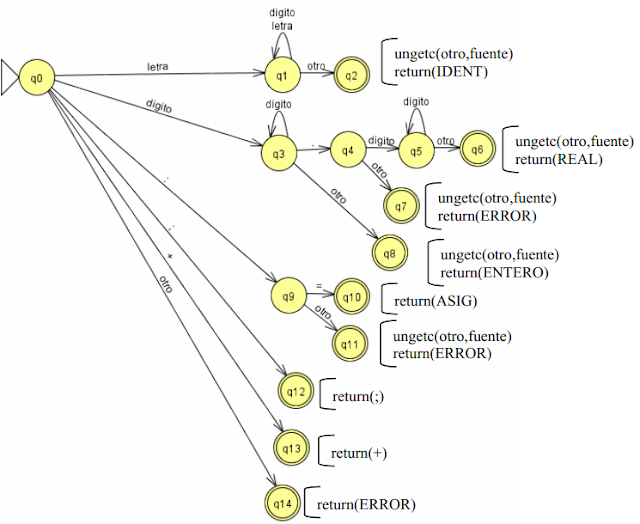
EJEMPLO 1. DIAGRAMA DE TRANSICIÓN

Se tiene un lenguaje de programación con los siguientes componentes básicos:

a.  Identififcador           letra(letra|digito)*

b.  Real sin signo           digito+.digito+

c.  Entero sin signo        digito+

d.  Asignador                 :=

e.  Fin de sentencia       ;

f.  Suma                       +

Nota: la función ungetc regresa un espacio en el archivo.

DIAGRAMA DE TRANSICIÓN

EJEMPLO 2. DIAGRAMA DE TRANSICIÓN

Para un lenguaje de programación de expresiones lógicas considerar los siguientes elementos:

a.  Identificador             letra(letra|digito)+

b.  Entero                      digito+

c.  Suma                        +

d.  Mayor que                 >

e.  Mayor o igual que      >=

f.  Leer                         READ

g.  Escribir                    WRITE

h.  Si                            IF

i.  Entonces                   THEN 

j.  Paréntesis Izquierdo  (

k.  Paréntesis Derecho    )

l.  Fin de Sentencias       ;

m.  Asignador                =

DIAGRAMA DE TRANSICIÓN

EJERCICIOS DIAGRAMAS DE TRANSICIÓN

PARA CADA EJERCICIO CREAR EL DIAGRAMA DE TRANSICIÓN Y LA TABLA DE TRANSICIÓN.

Se tiene un lenguaje de programación que tiene los siguientes componentes lexicos básicos:

Identififcador               letra(letra|digito)*

Real sin signo              digito+.digito+

Entero sin signo           digito+

Asignador                    :=

Fin de sentencia           ;

Suma                            +

Para un lenguaje de programación de expresiones lógicas considerar los siguientes elementos léxicos:

Identificador                 letra(letra|digito)+

Entero                           digito+

Suma                             +

Mayor que                    >

Mayor o igual que        >=

Leer                              READ

Escribir                         WRITE

Si                                  IF

Entonces                       THEN 

Paréntesis Izquierdo     (

Paréntesis Derecho       )

Fin de Sentencias          ;

Asignador                      =

Para un lenguaje de programación de expresiones lógicas considerar los siguientes elementos léxicos:

Entero         digito+

Suma           +

Producto      *

Suma           ++

Crear el DT y TT para los siguientes componentes léxicos:

Letras          Cualquier secuencia de una o más letras

Digitos         Cualquier secuencia de numeros enteros

Asignacion   =

Suma           +

Resta           -

Imprimir      print

Escribir        write

Publicado por: 
Pedro Antonio Villalta, perfil de Google+

https://plus.google.com/u/0/105223072803758915793/about